
Aplicación didáctica del problema de las #AgujasDeBuffon. #CEdRevistaDigitalDocente Clic para tuitearResumen: En este artículo se replantea el problema de Buffon estableciendo una relación directa entre proporcionalidad geométrica y probabilidades. Se presenta un breve repaso de algunas propuestas ya existentes seguidas de una ampliación adecuada para alumnos de 4º de ESO a través de teselas diferentes del plano. También se presenta una ampliación de las actividades para alumnos de bachillerato a través de un replanteo del problema en tres dimensiones, usando para ello generadores de números aleatorios.
Palabras clave: Buffon; 4º ESO; Bachillerato; Números aleatorios; Tesela; Tres dimensiones; Probabilidad teórica; Probabilidad empírica.
Abstract: This paper rethinks Buffon’s needle problem by establishing a direct relationship between geometric proportionality and probability. It presents a brief review of some already existing proposals followed by an expansion of these solutions through different tiles of the plane for students fit for students of this level. It also presents an extension of the activities for high school students through a reconsideration of the problem in three dimensions, using random number generators.
Keywords: Buffon; Secondary Education; Random numbers; Tile; Three dimensions; Theoretical probability; Empiric probability.
LAS AGUJAS DE BUFFON
Índice de contenidos
El problema de Buffon original
En un principio Georges Louis Leclerc, conde de Buffon, en su Historia Natural publicada en 1773 planteó el problema de calcular la probabilidad de que al lanzar una aguja de longitud l sobre una superficie con líneas paralelas separadas una distancia d, tocase alguna de las líneas.
La respuesta al problema de Buffon tiene diferentes soluciones dependiendo de la relación entre l y d, de tal modo que intuitivamente se puede deducir que cuanto más pequeña sea la aguja, menor será la probabilidad. Dicha intuición no constituye en ningún caso una demostración matemática, pero se tiene que tener en cuenta que dicha prueba escapa al objetivo del presente trabajo por cuanto supera por mucho el nivel de ESO y de Bachillerato. Se pueden encontrar diversas demostraciones en internet. Para el caso l=d, por ejemplo, la probabilidad es 2/π.
Revisión de propuestas existentes
La revisión que veremos dejará de lado simples menciones existentes en la bibliografía científica (por ejemplo, Hoffman, 1998) para centrarnos en algunas propuestas didácticas recientes, sin ánimo de exhaustividad pero sí para ilustrar el estado de la cuestión. Se trata de hacer un brevísimo repaso de lo que será nuestro punto de partida.
En el CREAMAT (Centro de recursos para enseñar y aprender las matemáticas, que depende de la Generalitat de Catalunya) se editó un video sobre una adaptación del problema de Buffon, en el que se muestran las tiradas de agujas sobre hojas de papel con líneas paralelas y del que el profesor Anton Aubanell, además, elaboró una ficha de trabajo, y el profesor Antoni Gomà, comentarios para el profesorado. Como ya hemos apuntado anteriormente, esta cuestión ha sido tratada formalmente en varios estudios, algunos de ellos online.
El interés que tiene esta adaptación es la relación estrecha que se establece entre probabilidades y geometría a través de la proporción de áreas, de tal modo que se muestran vínculos entre apartados de la asignatura de matemáticas que habitualmente parecen totalmente independientes.
La adaptación del CREAMAT se presenta en un doble sentido. En primer lugar, se propone una aproximación empírica del número π. Se trata de lanzar muchas veces una aguja (o palo) de longitud l sobre una hoja (o lienzo) con líneas separadas una distancia l. La proporción de agujas que tocan alguna línea en relación al número de
lanzamientos totales se debería aproximar a 2/π, y de ahí que se pueda obtener una aproximación de π mediante la expresión πaprox=2N/A, donde N es el número total de lanzamientos y A el número de veces que el palo ha tocado alguna línea. Existen aproximaciones usando este método mediante el uso de las TIC, y más particularmente del programa Geogebra.
En esta experiencia no se hace un cálculo aproximado de la probabilidad, sino que de lo que se trata es de calcular, como ya se ha dicho, una aproximación a un número irracional. No es este el objetivo del presente trabajo por cuanto no se puede demostrar al alumnado de forma comprensible el valor de dicha probabilidad y, por ese motivo, abandonaremos este sendero.
En segundo lugar, la otra propuesta que ofrece el CREAMAT es un replanteamiento del problema: lanzar una moneda sobre líneas o cuadrículas de forma totalmente aleatoria, calcular la probabilidad que la moneda toque alguna línea y luego hacer una comprobación empírica. Esta manera de trabajar permite establecer una conexión directa entre proporcionalidad geométrica y probabilidad, siendo de interés esta línea de razonamiento para el presente trabajo, y por tanto será este nuestro punto de partida.
Propuesta didáctica para 4º ESO
Lo que nos proponemos es, por un lado, el cálculo de la probabilidad teórica de que una moneda de 0,01€, al ser lanzada sobre un dibujo teselado (o mosaico) dibujado en una hoja de papel tamaño A3 toque alguna de las líneas dibujadas. Por el otro lado, se trata de hacer numerosos lanzamientos para ver qué tal buena es la aproximación de la probabilidad teórica a través de la probabilidad empírica. Es por este motivo que es aconsejable trabajar en grupos para así conseguir bastantes lanzamientos para este último cálculo.
La ubicación de esta actividad se podría plantear en diversos cursos de ESO, pero la madurez adquirida por el alumnado en 4º puede permitir una mayor comprensión de lo que se está haciendo, y en particular de la relación entre proporcionalidad geométrica y probabilidad. De hecho, estamos relacionando dos de las áreas descritas en la Orden ECD/65/2015, de 21 de enero, por la que se describen las relaciones entre las competencias, los contenidos y los criterios de evaluación de la educación primaria, la educación secundaria obligatoria y el bachillerato. En efecto, dentro de la competencia matemática existen las áreas “El espacio y la forma” y “La incertidumbre y los datos”, que se interconectan completamente en el presente artículo.
El planteamiento de esta actividad se puede llevar a cabo de diferentes modos, ya sea aportando el profesorado el dibujo sobre la que se tiene que lanzar la moneda, como haciendo que lo diseñe el alumnado. Si la elabora el profesorado, no es necesario que dé las medidas de las figuras que se representen. Llegados a este punto, se propone como ejemplo un caso en que se lleva a clase un teselado.
La siguiente figura representa algunos de los dibujos que se pueden proporcionar al alumnado (cada tipo en una hoja de papel diferente):
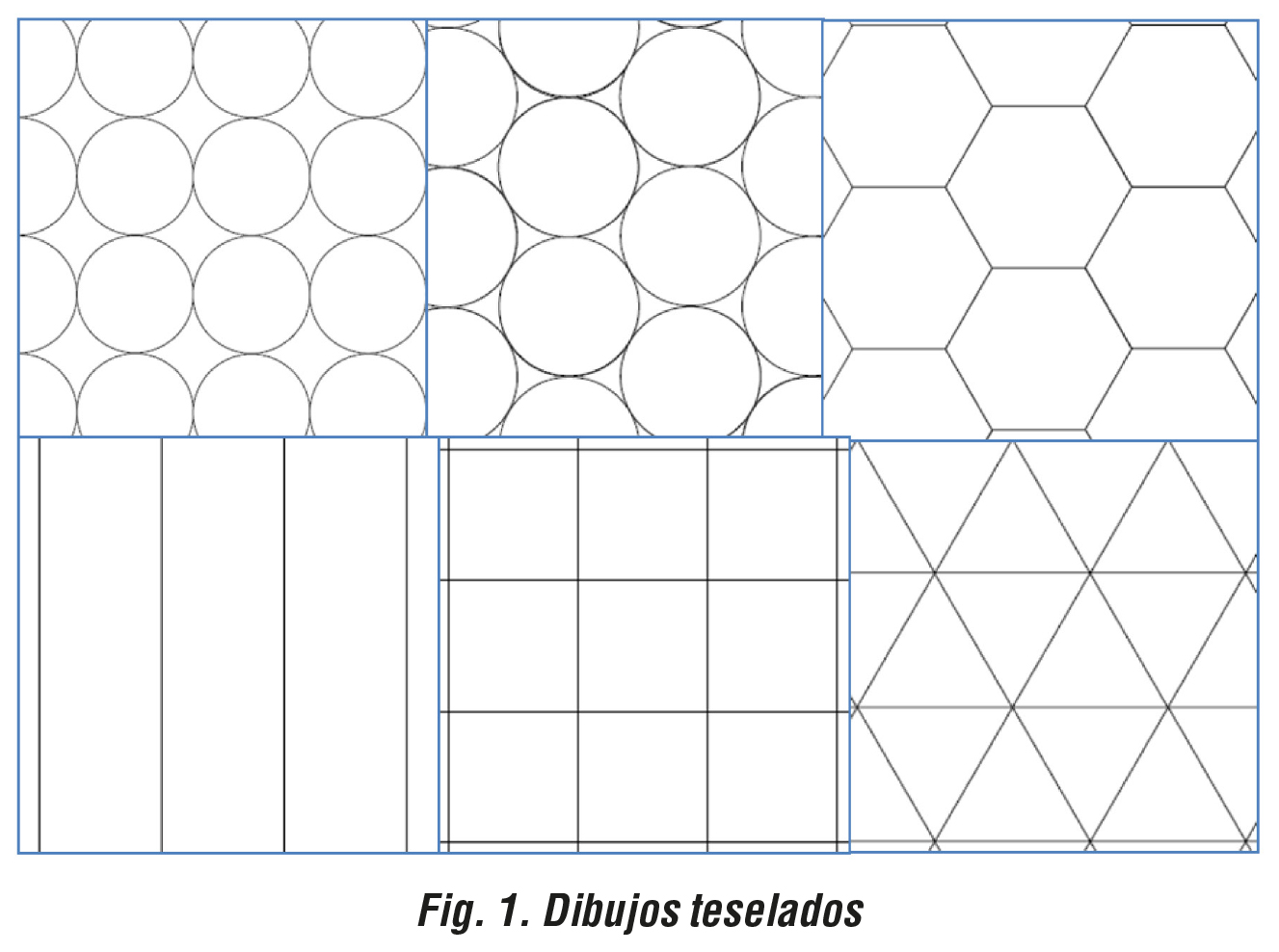
Se puede hacer, por ejemplo, que el diámetro de las circunferencias sea el doble del de la moneda, y que este hecho tenga que ser descubierto por el alumnado. Así, se pueden hacer mosaicos homotéticos o proporcionales para intentar establecer relaciones entre unos y otros.
Para calcular la probabilidad teórica, el alumnado tiene que deducir que se trata simplemente de un problema de proporcionalidad geométrica. Los pasos a seguir son:
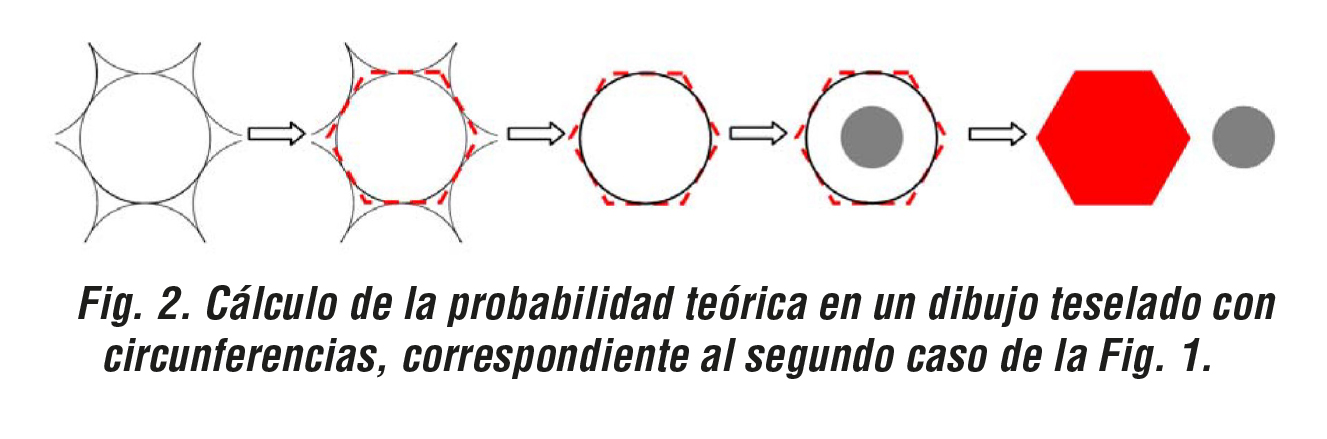
- Se tiene que calcular la pieza “mínima” (tesela) del mosaico que se va repitiendo (con alguna modificación en el caso de las líneas paralelas). Con idénticas teselas, puestas en la posición conveniente, se tiene que poder reconstruir el mosaico entero, sin que se superpongan ni que queden huecos. Los casos más complejos de entre los propuestos en la Figura 1 son los de las circunferencias, ya que la pieza “mínima” en el primer caso es un cuadrado (que no está dibujado) y en el segundo caso un hexágono regular (se pueden considerar figuras más pequeñas, como por ejemplo, en el segundo caso, triángulos regulares, pero no resulta tan intuitivo para el alumnado y pese a que se pueden hacer los cálculos posteriores del mismo modo, le podría resultar menos visual. De ahí el entrecomillado de la palabra “mínima”).
- Se tienen que tomar las medidas adecuadas de esta tesela para poder calcular su área. En la Figura 2 será el área del hexágono.
- Se tiene que medir el radio de la moneda (este paso es opcional, pero recomendable).
- Se tiene que dibujar y calcular el área, dentro de la tesela, de la zona en que se puede situar el centro de la moneda sin que ésta toque ninguna línea. En la Figura 2 será el área del círculo sombreado.
- La probabilidad teórica es 1 menos el cociente entre el área de la pieza “mínima” y el área de la zona en que puede caer el centro de la moneda sin que toque ninguna línea.
El cálculo de la probabilidad empírica es muy sencillo ya que se trata de ir lanzando la moneda y averiguar la frecuencia relativa de las veces que esta toca alguna línea.
Más adelante se propondrá una ficha de trabajo con las pautas necesarias para que el alumnado pueda trabajar y llegar por sí mismo a las conclusiones correctas. Además, se espera que cada grupo haga una exposición oral donde explique todo el proceso que ha llevado a cabo así como los resultados obtenidos.
Propuesta didáctica para Bachillerato
La propuesta que se hace para Bachillerato va mucho más allá, ya que se desarrollará de forma totalmente virtual. La tesela plana, en este caso, se tiene que transformar en una malla tridimensional mediante hexaedros, paralelepípedos o esferas análogamente a lo que habíamos hecho en el plano (también se puede considerar un haz de planos paralelos). La moneda, a su vez, se transformará en una esfera.
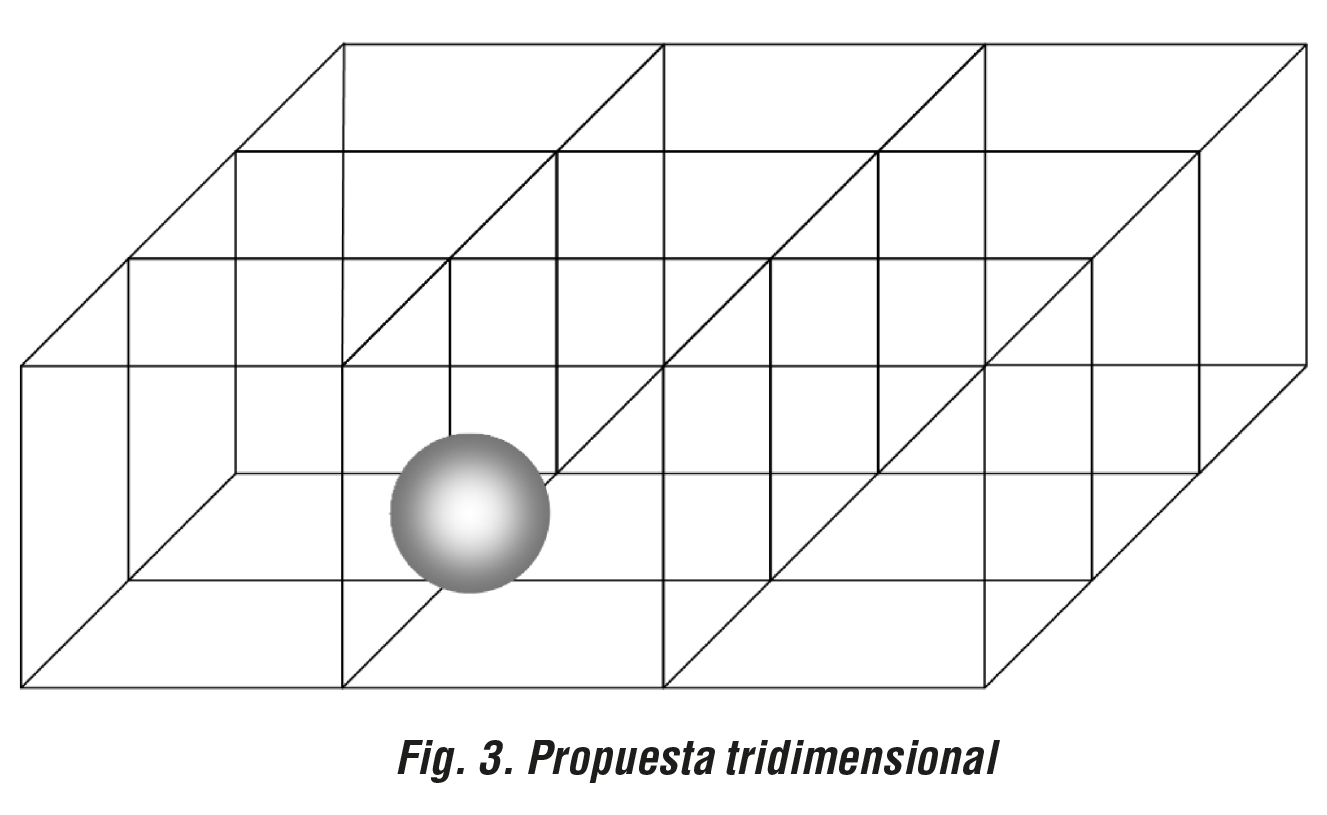
La probabilidad teórica de que al lanzar una bola (suponiendo que esta puede quedar suspendida en el aire) y que toque una cara de la malla tridimensional se calcula de forma análoga como se hacía en el plano, pero donde antes se buscaban áreas, ahora se buscarán volúmenes.
La dificultad, en cambio, aparece en el cálculo de la probabilidad empírica, puesto que el supuesto de que la bola pueda quedar suspendida en el aire es ciencia ficción. Se puede simplificar el cálculo trabajando solo con una pieza “mínima” tridimensional. Hecho esto, será necesario establecer un sistema de coordenadas y calcular el rango en que se puede mover la bola sin tocar ninguna cara de la malla.
A partir de aquí el lanzamiento de la bola se tendrá que convertir en una generación aleatoria de ternas dentro del rango de coordenadas en que hayamos situado la pieza “mínima”. Hecha esta parte, la más complicada sin duda, la probabilidad empírica vuelve a ser un simple cálculo de frecuencia relativa.
La inserción de esta actividad en el nivel de Bachillerato queda totalmente justificada por el uso necesario de los sistemas de coordenadas en tres dimensiones y por la parametrización necesaria en aras de poder establecer los rangos en los que se puede mover, por un lado, el generador de números aleatorios y, por el otro, el centro de la esfera virtual con la que se trabajará.
Se requieren, además, conocimientos informáticos para trabajar con métodos iterativos de generación de coordenadas aleatorias, conteo de casos favorables o análogos que permitan trabajar esta actividad.
Papel del profesorado en la actividad
A la hora de llevar a cabo esta actividad en ESO, en un primer momento el profesorado tiene que conocer el nivel de conocimiento de la materia, así como las aptitudes del alumnado para componer los grupos de trabajo. Una opción es trabajar con grupos homogéneos y otra con grupos heterogéneos. Ambas opciones son plausibles en el trabajo aquí propuesto, pero se tiene que tener en consideración qué ejercicios tiene que hacer cada agrupación según la tipología de alumnado que la compone.
En el caso de que se trabaje con grupos homogéneos se debiera considerar dar teselas según la posibilidad de que el alumnado pueda llegar al resultado deseado. Durante todo el proceso de trabajo, el profesor tendrá que poner especial atención a los grupos con mayor dificultad para que puedan avanzar, sin que eso signifique que no tenga que observar también al resto para ver si avanzan por buena senda. En cambio, si los grupos sonheterogéneos se pueden dar diversas teselas a cada grupo teniendo en cuenta, también su composición.
En un primer momento, una vez hechos los grupos, el profesorado tiene que explicar la actividad y lo que se espera que consiga el alumnado, pero sin necesidad de dar muchas pistas. A continuación, se dan las teselas, la moneda y alguna ficha como la que se propondrá en el apartado siguiente.
Cuando el alumnado empiece a trabajar el profesorado tiene que ser un mero acompañante, observando los pasos de aquél y simplemente dando pistas de resolución en caso de que vea que se ha encallado o que ha cometido algún error. En ningún caso se espera que sea el profesorado quien resuelva la actividad. Es importante que observe, y si de da el caso aconseje, en situaciones en que los resultados sean divergentes (cosa que no significa que sean incorrectos), como por ejemplo cuando las medidas tomadas fallen por algún milímetro o cuando las probabilidades empíricas obtenidas sean (y en general lo serán) diferentes.

Para el caso de Bachillerato, también es aconsejable trabajar en grupos. Aunque al alumnado de este nivel se le pueda suponer autonomía, la actividad puede tener tanta complejidad como para que se le vaya haciendo alguna explicación a lo largo del proceso. Aparte del cálculo de las probabilidades empírica y teórica, será importante que descubran que el sistema de referencia que escojan no altera los resultados, de tal manera que si por ejemplo se trabaja con una malla como la de la Figura 3 es suficiente suponer que el lado de cada cubo mide 1 unidad (habrá que transformar convenientemente la esfera, evidentemente, pero es muy sencillo y más cuando se trabaja con el ordenador).
Ficha de trabajo para 4º ESO
La ficha que se dé a los alumnos puede tener un contenido como el siguiente, que es meramente orientativo. En el caso de grupos homogéneos no todos han de contestar todas las preguntas sobre todo las más complicadas, como puede ser la número 6.
- Tira la moneda 100 veces sobre el mosaico proporcionado.
- ¿Cuántas veces ha tocado alguna línea en tu caso?
- ¿Qué probabilidad experimental has obtenido?
- ¿Cuántas tiradas ha hecho tu grupo?
- ¿Cuántas veces ha tocado la línea la moneda en el grupo?
- ¿Cuál es la probabilidad experimental obtenida por el grupo?
- ¿Existen diferencias significativas entre tus resultados y los del grupo? En caso afirmativo, ¿a qué crees que se deben? ¿Qué papel crees que juega el azar?
- ¿Es posible que después de tirar 100 veces la moneda no toque nunca alguna línea? ¿Sería creíble? ¿Es lo mismo probable que posible?
- Representa el mosaico y decide cual sería una pieza mínima con la que lo podrías ir construyendo todo, en la posición conveniente, sin que haya superposiciones ni espacios vacíos. Calcula su área.
- Calcula el radio de la moneda. ¿Existe alguna relación entre el valor obtenido y los que has obtenido en la pregunta anterior?
- Sobre la pieza mínima que has obtenido antes, sombrea la parte donde puede estar el centro de la moneda sin que toque ninguna línea. Calcula su área.
- Calcula la probabilidad de que al tirar la moneda sobre el mosaico toque alguna línea.
- A partir de lo que llevas hecho, calcula la probabilidad anterior cuando los lados de las piezas del mosaico miden k (para el caso de líneas paralelas k es la separación que hay entre ellas y para el caso de circunferencias k es su diámetro) y el diámetro de la moneda es d.
Propuesta de ampliación
Para el caso de 4º de la ESO se puede proponer al alumnado el diseño de sus propios dibujos teselados. Esta es una actividad puramente geométrica pero ilustrativa de los diferentes diseños que se pueden dar a un mosaico. Puede ser interesante ver que en el fondo puede llegar a ser irrelevante el dibujo planteado a la hora de calcular su área, ya que la tesela básica se puede transformar en un triángulo, cuadrado o hexágono, por la teoría de los grupos cristalográficos planos. En el caso tridimensional también se puede plantear, aunque después la resolución del problema se complique porque sea prácticamente imposible, establecer una parametrización adecuada de la zona en que puede ir la bola sin que toque ninguna cara.
Es posible que el alumnado plantee, vista la variedad de dibujos que se pueden presentar, si también es factible modificar la forma de la moneda o de la bola. En este caso el problema se complica a la hora de calcular la pobabilidad teórica, de tal modo que el nivel de ESO y de Bachillerato no permite su resolución ya que no solo será relevante donde haya caído la figura, sino también en qué posición.
En este caso la ampliación de la actividad se puede restringir al cálculo empírico aunque no para el caso tridimensional, ya que en este caso determinar la forma en que se sitúa la figura es mucho más complicada.
En este artículo se ha pretendido abrir el problema de Buffon a un abanico de posibilidades, tratando únicamente de dar ideas para que se puedan trabajar en el aula si se cree conveniente.
Será tarea del profesorado, si quiere lanzarse a esta labor, concretar la tipología de cada actividad, de tal modo que hasta en grupos diferentes puede proponer tareas diferentes.
Lo que sí se ha pretendido es que una vez preparado el trabajo, se dé la máxima autonomía al alumnado, con una observación constante pero no invasiva de su trabajo.
Te puede interesar…
Artículo completo
El artículo Las Agujas de Buffon. Aplicación didáctica para E.S.O y Bachiller forma parte del número 11 de Campus Educación Revista Digital Docente un proyecto destinado a la divulgación de publicaciones de carácter educativo que permite la difusión del conocimiento y pretende el enriquecimiento de toda la comunidad educativa.
Otros números
Puedes consultar los números anteriores de Campus Educación Revista Digital Docente, la revista educativa que lleva a sus espaldas once entregas repletas de artículos de corte científico-didáctico de manos de docentes comprometidos, que desean exponer sus conocimientos educativos y ser de ayuda al resto de compañeros de profesión.
- Campus Educación Revista Digital Docente Nº 1
- Campus Educación Revista Digital Docente Nº 2
- Campus Educación Revista Digital Docente Nº 3
- Campus Educación Revista Digital Docente Nº 4
- Campus Educación Revista Digital Docente Nº 5
- Campus Educación Revista Digital Docente Nº 6
- Campus Educación Revista Digital Docente Nº 7
- Campus Educación Revista Digital Docente Nº 8
- Campus Educación Revista Digital Docente Nº 9
- Campus Educación Revista Digital Docente Nº 10
Publica con nosotros
Campus Educación Revista Digital Docente ofrece la posibilidad a la comunidad docente de publicar artículos científicos y didácticos de forma totalmente gratuita, permitiendo así la divulgación del quehacer profesional docente, contribuyendo al avance de las Ciencias de la Educación.
Los autores de Campus Educación Revista Digital Docente ven en este medio un lugar ideal para la investigación pedagógica, a la vez que reciben un certificado de autoría que les puede ayudar a sumar puntos en diferentes procesos selectivos y baremo de méritos, como en las Oposiciones Docentes o el Concurso General de Traslados.
Pueden conseguirse 4 certificaciones gratuitas en Campus Educación Revista Digital Docente en los siguientes casos:
- Si eres alumno de alguno de nuestros Másteres Oficiales Universitarios
- Si has hecho 4 o más cursos homologados para Oposiciones y CGT con Campuseducacion.com
- Si eres alumno del Centro de Estudios Campus Educación
Para los afiliados de ANPE Albacete y ANPE Castilla-La Mancha las certificaciones son gratuitas en todos los artículos.





